Fibonacci Funhouse: Exploring Ruby Algorithms for Fibonacci Numbers

This article is a deep dive into the world of Fibonacci numbers to show some really neat tools that Ruby provides. Some may not be used very often, but it is always good to have them in your toolbox.

So using Ruby, what is the largest Fibonacci number we can calculate quickly?

Understanding the Fibonacci Sequence

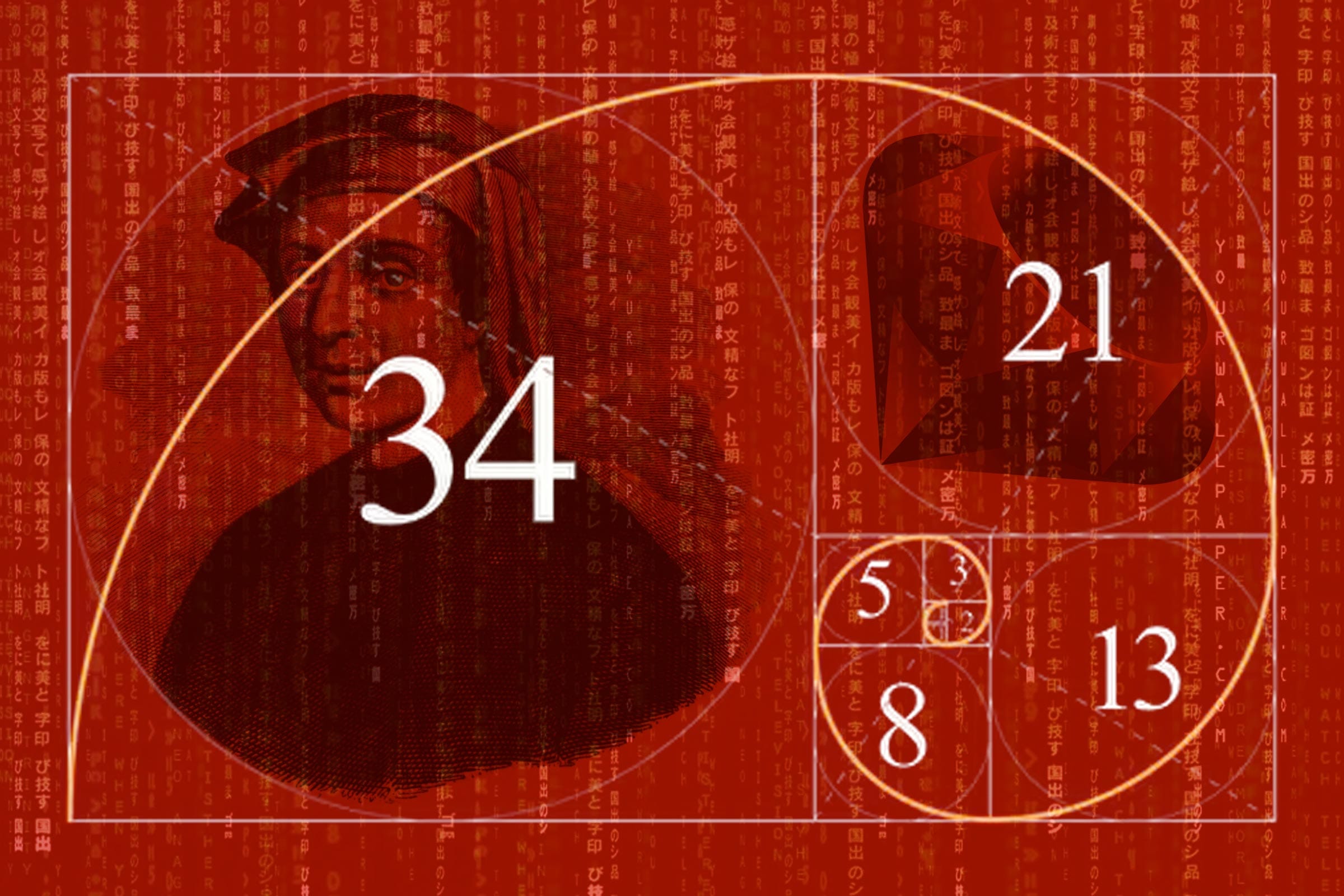
In case you are not familiar, the Fibonacci sequence is a classic mathematical progression where each number is the sum of the previous two. Starting with 0 and 1, the sequence looks like this:

$$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …$$

Basic Recursive Fibonacci Algorithm and Its Limitations

The most straightforward method to compute Fibonacci numbers is a simple recursive function:

def fibonacci(n)
  return 0 if n == 0
  return 1 if n == 1

  fibonacci(n - 1) + fibonacci(n - 2)
end

This algorithm is simple and clear. However, if we look at its performance, we can see that it starts out fine, but once we cross the 30th Fibonacci number, the performance starts to degrade exponentially.

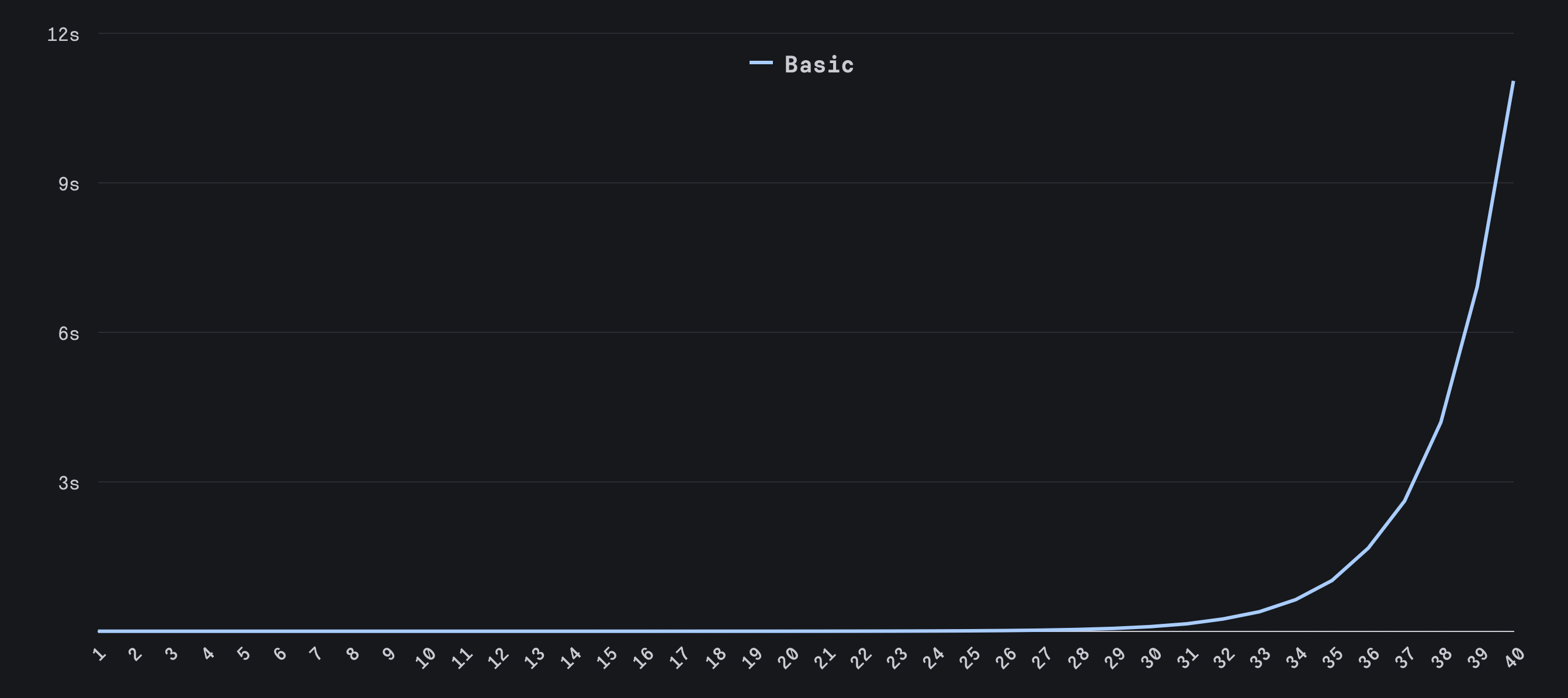
This happens because we are doing a lot of redundant calculations. Imagine calculating the 5th Fibonacci number. To calculate it, we need the 4th and the 3rd numbers. To calculate the 4th number, we need the 3rd and the 2nd. This pattern repeats until we hit the 0th or the 1st number. The larger the number, the more computations we need to perform.

Using Binet’s Formula for Constant Time Calculation

It turns out there is a closed-form expression for calculating the nth Fibonacci number. To overcome recursive inefficiency, we turn to Binet’s formula:

$$F_n = \frac{\phi^n - \psi^n}{\sqrt{5}}$$

Where:

• \$\phi = \frac{1 + \sqrt{5}}{2}\$, (phi) the golden ratio,
• \$\psi = \frac{1 - \sqrt{5}}{2}\$, (psi) its conjugate.

This formula allows computation in constant time, a significant performance leap. Implementing it in Ruby involves calculating powers of irrational numbers and rounding the result.

In fact, since \$\psi^n\$ is so small, we can further simplify this formula to:

$$F_n = \Bigl\lfloor\frac{\phi^n}{\sqrt{5}}\Bigr\rceil$$

Closed-form Algorithm

SQRT_FIVE = Math.sqrt(5)
PHI = (1 + SQRT_FIVE) / 2

def fibonacci(n)
  ((PHI**n)/SQRT_FIVE).round
end

This is a constant-time algorithm according to our performance graphs.

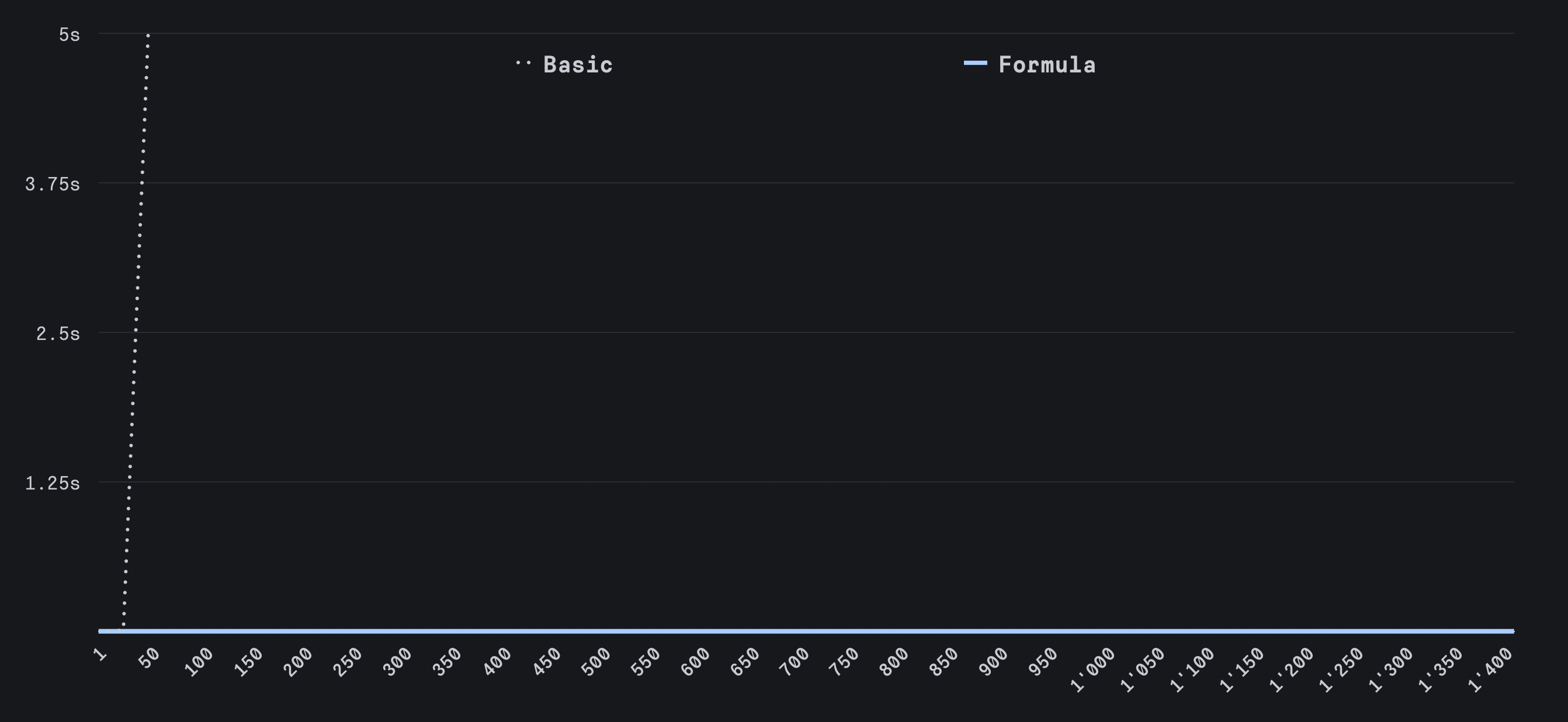
However, this algorithm faces two major challenges:

1. Precision limits: At the 71st Fibonacci number, this algorithm will return a value of \$608061521170130\$, whereas the actual 71st Fibonacci number is \$608061521170129\$ — just one less.

   This happens because Ruby does not have infinite precision, so at some point, rounding issues occur. As the algorithm calculates larger Fibonacci numbers, this discrepancy increases.

2. Float domain errors: At around the 1475th Fibonacci number, this algorithm will raise a FloatDomainError.

   This occurs in Ruby when a calculation exceeds the limits of floating-point precision and returns Infinity. For example, raising \$\sqrt{5}\$ to the 883rd power yields Infinity, and calling methods like round on Infinity will trigger a FloatDomainError.

   Math.sqrt(5) ** 883
   => Infinity
   

Can we do better?

Closed-form Algorithm #2

Ruby’s BigDecimal library offers arbitrary-precision decimal arithmetic, allowing us to mitigate rounding errors by specifying how many decimal places to calculate.

By replacing standard floating-point operations with BigDecimal, we can compute Fibonacci numbers with much greater accuracy and avoid early overflow issues.

SQRT_FIVE = BigDecimal("5").sqrt(1000)
PHI = (1 + SQRT_FIVE) / 2

def fibonacci(n)
  ((PHI**n)/SQRT_FIVE).round
end

This is already much better! We can compute the correct Fibonacci numbers well past the 75th. The trade-off is performance: the more precision requested, the slower the calculations become.

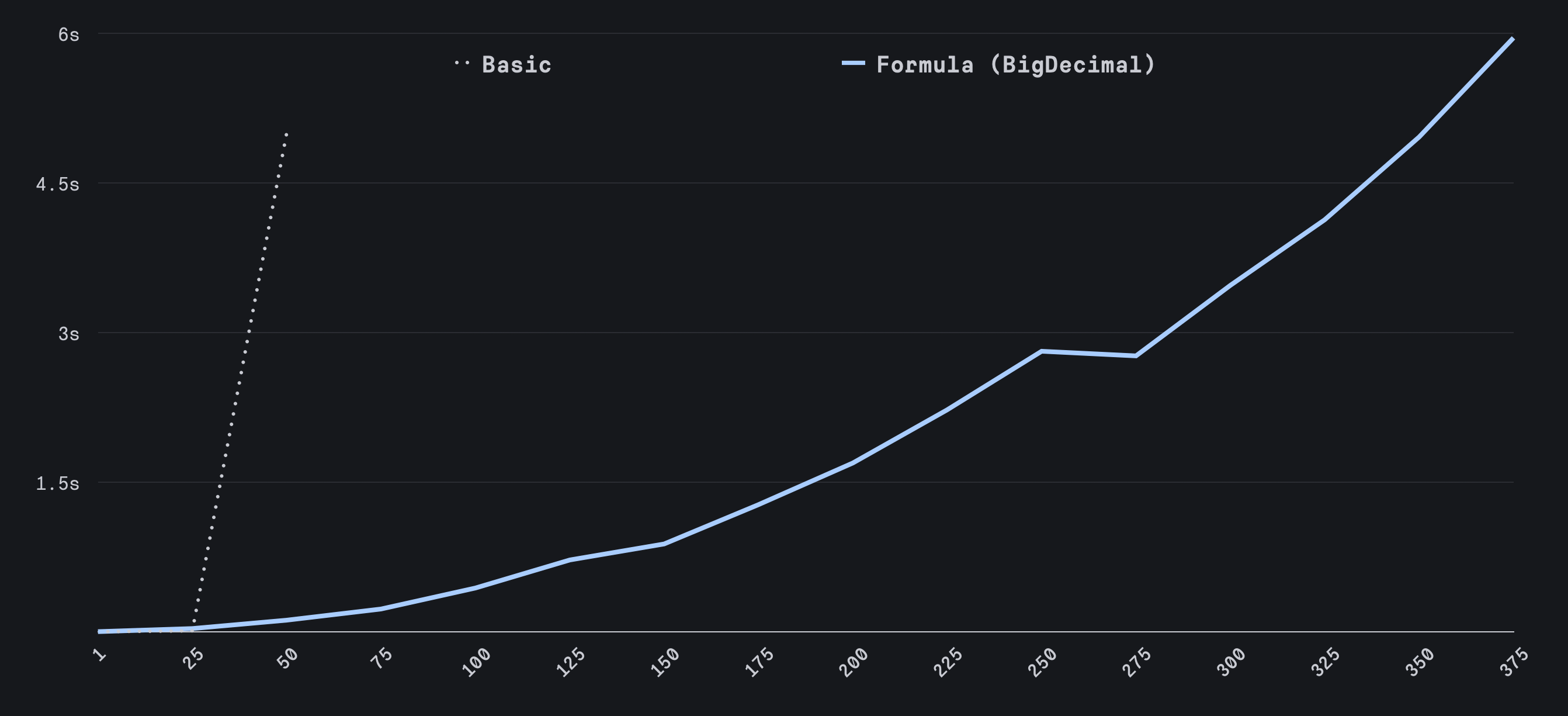
BigDecimal is a great library to leverage in Ruby. It is a little slower than the standard numeric options, but it avoids many of the precision pitfalls.

This gets us past the 100th Fibonacci number. What do we need to do to get to the 1000th?

Closed-form Algorithm #3

Ruby’s built-in support for rational numbers provides a promising alternative. Instead of decimals, rationals represent numbers as fractions of integers, avoiding floating-point precision problems.

\$\sqrt{5}\$ is an irrational number – it has a decimal expansion that doesn’t terminate nor repeat. However, we can approximate it:

$$\sqrt{5} = 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \ddots}}}}$$

Using continued fractions, we can approximate irrational numbers like \$\sqrt{5}\$ to arbitrary precision by expanding the fraction deeper and deeper.

$$\sqrt{5} = 2.23606797749978969640\dots$$

If we take this approximation a few levels deep, we get \$\frac{38}{17}\$, which is about \$2.235294117647059\$.

Going one level deeper gives us \$\frac{161}{72}\$, or approximately \$2.2361111111111\$. Each level brings a better approximation. We can see that in the error column of the following table. As we approximate \$\sqrt{5}\$ to a deeper level, the error between the rational representation and the real value will get smaller and smaller.

Depth	Rational	Error
0	\$\frac{2}{1}\$	0.2360679774997896964
1	\$\frac{9}{4}\$	-0.013932022500210303
2	\$\frac{38}{17}\$	0.0007738598527308728
3	\$\frac{161}{72}\$	-0.000043133611321414
4	\$\frac{682}{305}\$	0.0000024037292978931
5	\$\frac{2889}{1292}\$	-0.000000133955318662
6	\$\frac{12238}{5473}\$	0.0000000074650738184
7	\$\frac{51841}{23184}\$	-0.000000000416014306
8	\$\frac{219602}{98209}\$	0.0000000000231836827
9	\$\frac{930249}{416020}\$	-0.000000000001291982
10	\$\frac{3940598}{1762289}\$	0.0000000000000719997

We can achieve a good representation of \$\sqrt{5}\$ by going 1000 levels deep:

APPROXIMATION_DEPTH = 1000
SQRT_FIVE = 2 +
  APPROXIMATION_DEPTH.times.inject(0) do |result, _|
    Rational(1, 4 + result)
  end
PHI = (1 + SQRT_FIVE) / 2

def fibonacci(n)
  (PHI**n/SQRT_FIVE).round
end

This gets us well past the 1000th Fibonacci number quickly!

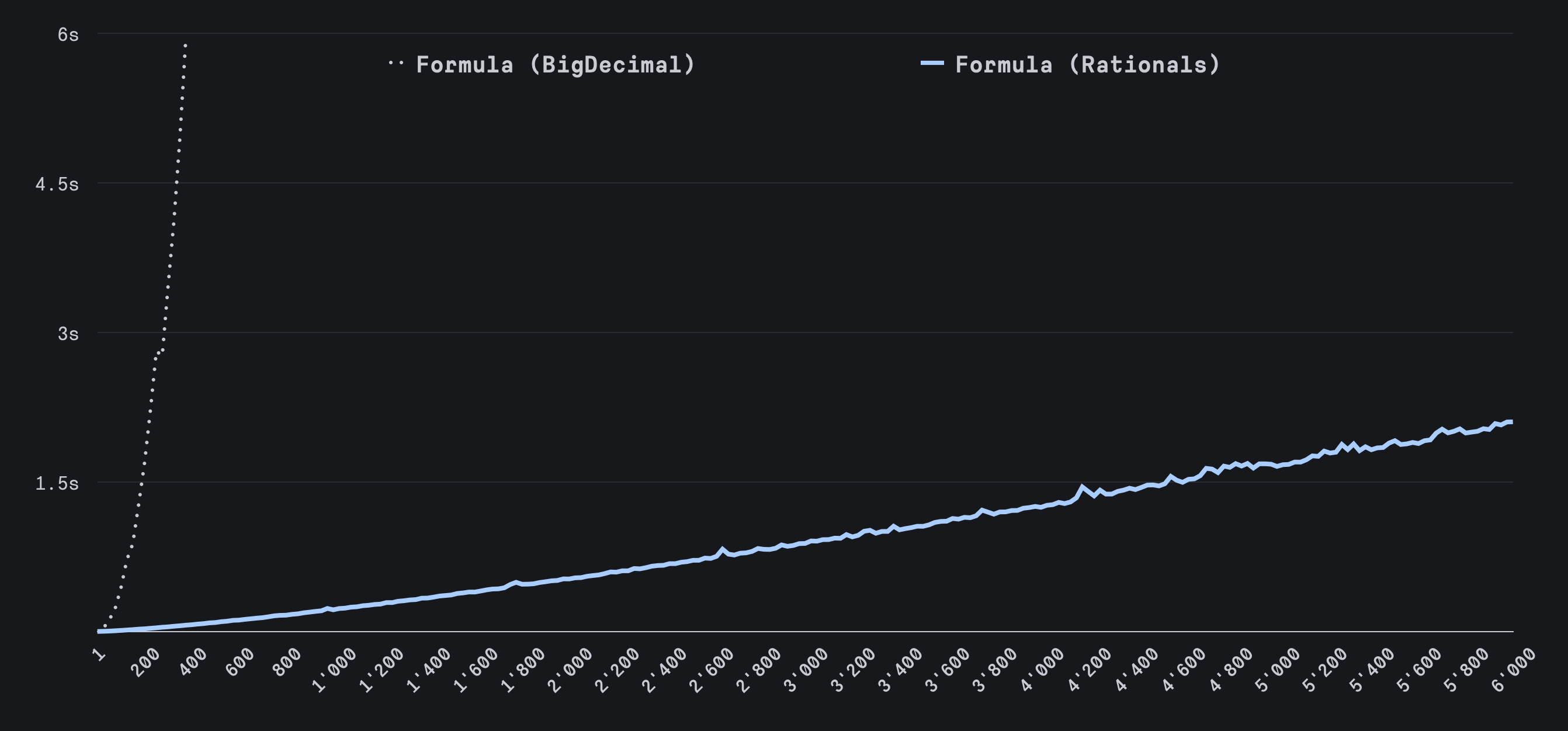
However, there are still limitations. Since we are using an approximation, the results start to drift as we seek larger Fibonacci numbers. In theory, we could use a deeper continued fraction to improve accuracy, but eventually, the numerator and denominator become so large that Ruby will raise a FloatDomainError again.

Rational numbers strike a good balance between precision and performance, making them a powerful tool in the Fibonacci algorithm toolbox.

How about the 10,000th Fibonacci number? Can we quickly calculate that?

Optimizing Recursion with Tail Call Optimization

To get further, we can come back to our original recursion method and make some improvements there. One way to do this is to eliminate redundant calculations.

# fibonacci.rb
def fibonacci(n, a = 0, b = 1)
  return a if n == 0
  return b if n == 1

  fibonacci(n - 1, b, a + b)
end

Unfortunately, this algorithm has one problem. At some point, the Fibonacci number will be too large and Ruby will raise a SystemStackError. This error typically occurs with infinite recursion. While this algorithm doesn’t recurse indefinitely, Ruby may not recognize that, and the growing stack can trigger an error.

We can improve efficiency by using a lesser-known feature called tail call optimization (TCO). TCO allows a recursive method whose last action is calling itself to reuse the current stack frame instead of creating a new one, effectively turning recursion into iteration.

In Ruby, tail call optimization is disabled by default but can be enabled with a small VM instruction tweak. This allows us to compute Fibonacci numbers for much larger inputs (up to hundreds of thousands) without encountering stack overflows.

# fibonacci.rb
def fibonacci(n, a = 0, b = 1)
  return a if n == 0
  return b if n == 1

  fibonacci(n - 1, b, a + b)
end

# main.rb
RubyVM::InstructionSequence.compile_option = {
  tailcall_optimization: true,
  trace_instruction: false
}
require_relative './fibonacci'

This is significantly better than any of the formulas we’ve seen so far! Not only can we calculate the 10,000th Fibonacci number quickly, but we can blow past the 100,000th number too!

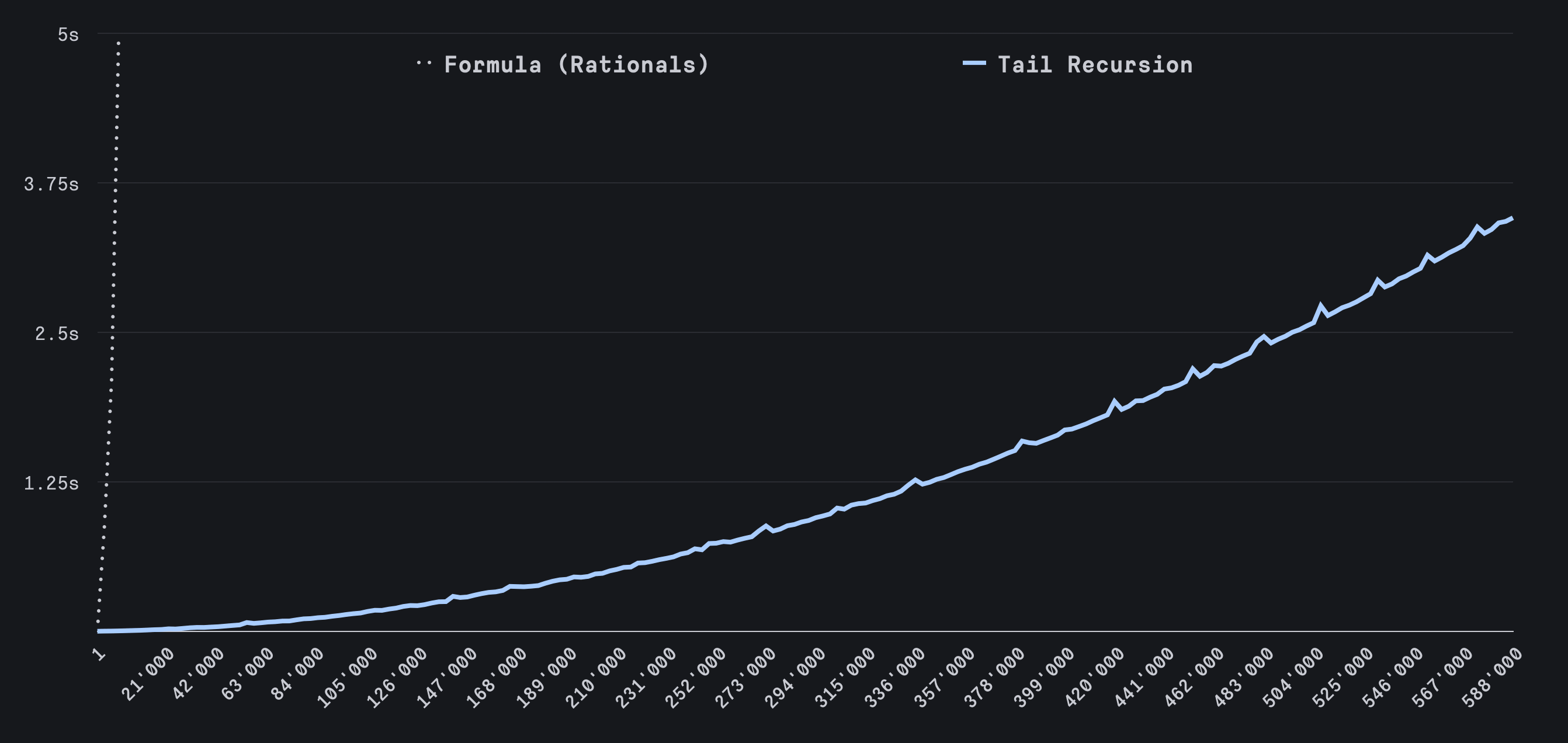
While powerful, TCO requires careful coding to ensure the recursive call is in tail position and can complicate debugging. I’ve never had a case where I needed to use it, but it’s still really neat to see this kind of feature in Ruby.

Can we calculate the 1,000,000th Fibonacci number?

Matrix Multiplication: A Mathematical Approach

To go further, we need to switch our focus to matrices. A matrix is just a two-dimensional grouping of numbers. For instance, this is a 2x3 matrix containing six elements:

$$ \begin{pmatrix} 1 & 9 & -13 \newline 20 & 5 & -6 \end{pmatrix} $$

Matrices have a special way of performing multiplication. It works by taking the leftmost value in a row of the first matrix, multiplying it by the topmost value in a column of the second matrix, then proceeding through the rest of the row and column, and finally summing those values together:

$$ \begin{pmatrix} a_1 & a_2 \newline a_3 & a_4 \end{pmatrix} \begin{pmatrix} b_1 & b_2 \newline b_3 & b_4 \end{pmatrix} = \begin{pmatrix} a_1b_1 + a_2b_3 & a_1b_2 + a_2b_4 \newline a_3b_1 + a_4b_3 & a_3b_2 + a_4b_4 \end{pmatrix} $$

It turns out there’s a Fibonacci identity involving matrices. Using a special 2x2 matrix:

$$ \begin{pmatrix} 1 & 1 \newline 1 & 0 \end{pmatrix}^n = \begin{pmatrix} F_{n+1} & F_n \newline F_n & F_{n-1} \end{pmatrix} $$

We can see how if we have a matrix with the corresponding Fibonacci numbers and we multiple it by this special 2x2 matrix, we end up with the next Fibonacci matrix in the series:

$$ \begin{aligned} \begin{pmatrix} F_{n+1} & F_{n} \newline F_{n} & F_{n-1} \end{pmatrix} \begin{pmatrix} 1 & 1 \newline 1 & 0 \end{pmatrix} & = \begin{pmatrix} F_{n+1} + F_n & F_{n+1} \newline F_{n} + F_{n-1} & F_n \end{pmatrix} \newline & = \begin{pmatrix} F_{n+2} & F_{n+1} \newline F_{n+1} & F_n \end{pmatrix} \end{aligned} $$

If we take this 2x2 and raise it to the power of \$n\$, the resulting matrix contains the n+1st, 2 copies of the nth, and the n-1st Fibonacci numbers.

We can implement this in Ruby using the Matrix library:

FIB_MATRIX = Matrix[
  [1, 1],
  [1, 0],
]
def fibonacci(n)
  return 0 if n == 0
  return 1 if n == 1

  result = n.times.inject(Matrix.I(2)) do |acc|
    acc * FIB_MATRIX
  end

  result[0, 1]
end

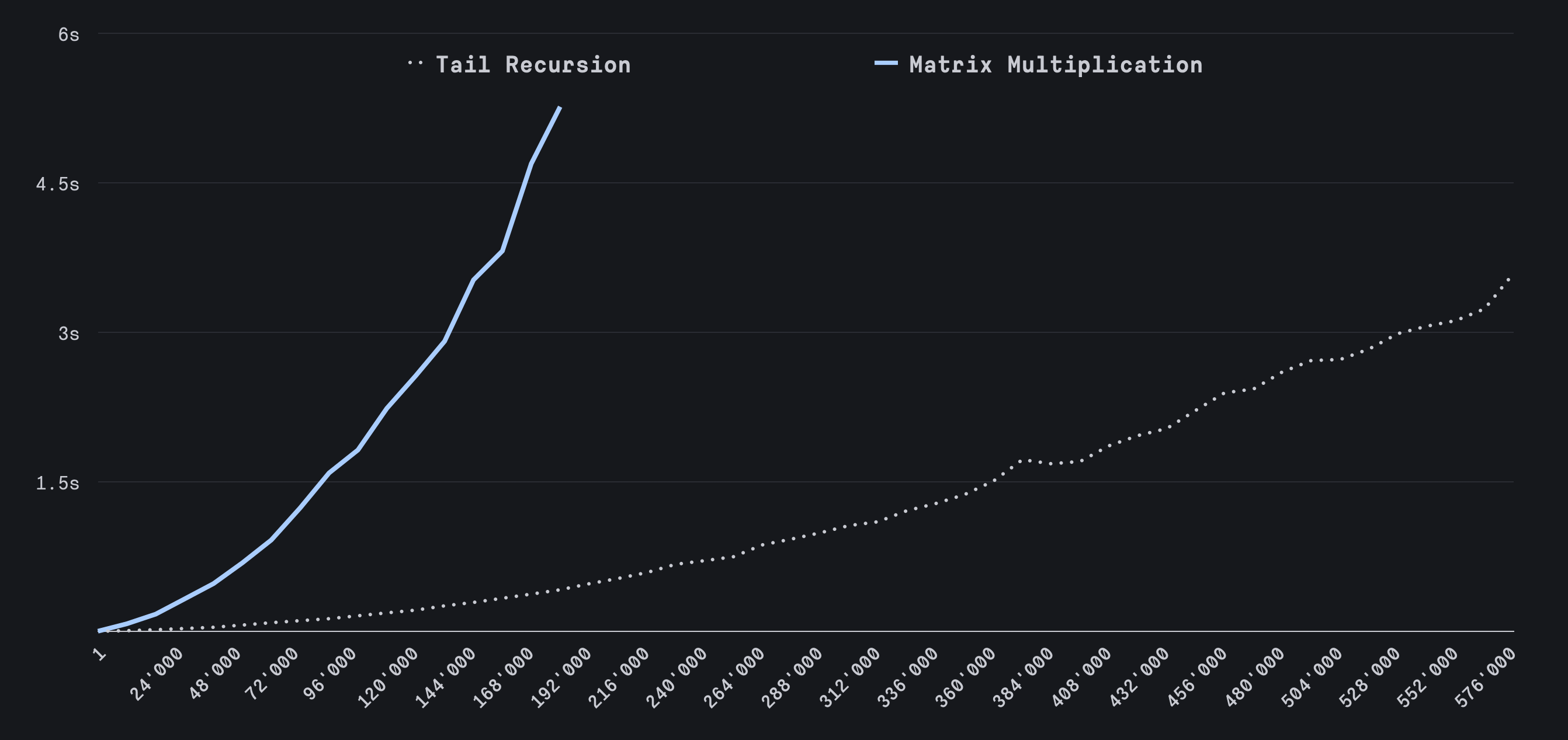
This algorithm is actually slower than our recursive version. However, we can refine it. By leveraging properties of matrix exponentiation, we can reduce the number of operations. Specifically, we can break down the exponent into powers of two, compute those powers individually, and multiply the results. For example, instead of raising the Fibonacci matrix to the 11th power, we could break that finding this matrix raised to the 8th, 2nd, and 1st power, and then multiple the results.

$$ \begin{aligned} \begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix} ^ {11} & = \begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix} ^ {8 + 2 + 1} \newline & = \begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix} ^ {8} \begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix} ^ {2} \begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix} ^ {1} \newline & = \begin{pmatrix} 31 & 21 \newline 21 & 13 \newline \end{pmatrix} \begin{pmatrix} 2 & 1 \newline 1 & 1 \newline \end{pmatrix} \begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix} \newline & = \begin{pmatrix} 144 & 89 \newline 89 & 55 \newline \end{pmatrix} \end{aligned} $$

We can rewrite our algorithm using this fact. This is known as the repeated squares algorithm:

FIB_MATRIX = Matrix[
  [1, 1],
  [1, 0],
]
def fibonacci(n)
  result = Matrix.I(2)
  base = FIB_MATRIX
  while n > 0
    result *= base if (n & 1) == 1
    base *= base if n > 1
    n >>= 1
  end
  result[0, 1]
end

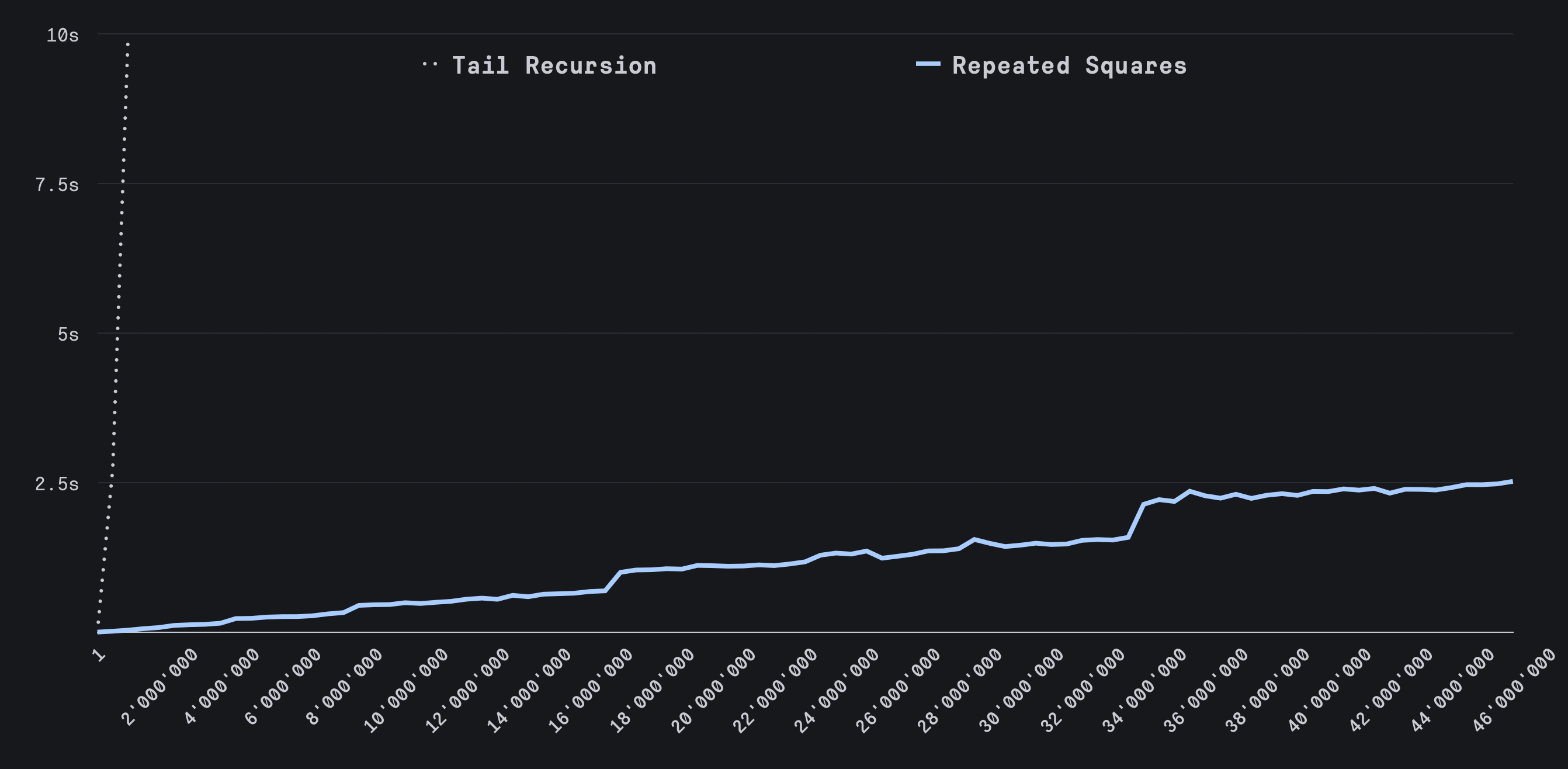
This approach allows us to calculate the 1,000,000th Fibonacci number and even above 45,000,000th Fibonacci number efficiently.

Understanding Ruby’s bitwise operators is incredibly useful for this method. They can be used in many contexts, such as generating random numbers that incorporate the current time, or toggling boolean configuration flags.

45,000,000th Fibonacci number is an impressively large. But can we go even further?

Fast Doubling Algorithm

The final leap comes from the fast doubling method. This approach uses matrix identities to reduce redundant calculations by computing two Fibonacci numbers at once, dividing the problem into halves. Consider the following:

$$ \begin{aligned} \begin{pmatrix} F_{2n+1} & F_{2n} \newline F_{2n} & F_{2n-1} \newline \end{pmatrix} & = \begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix}^{2n} & = \left(\begin{pmatrix} 1 & 1 \newline 1 & 0 \newline \end{pmatrix}^{n}\right)^2 \newline & & = \begin{pmatrix} F_{n+1} & F_n \newline F_n & F_{n-1} \newline \end{pmatrix}^2 \newline & & = \begin{pmatrix} F_{n+1}^2 + F_n^2 & 2F_nF_{n+1} - F_n^2 \newline 2F_nF_{n+1} - F_n^2 & F_n^2 + F_{n-1}^2 \newline \end{pmatrix} \end{aligned} $$

From this, we can see that:

$$F_{2n+1} = F_{n+1}^2 + F_n^2$$

$$F_{2n} = 2F_nF_{n+1} - F_n^2$$

This effectively gives us a formula for odd and even Fibonacci numbers. Here’s the final algorithm using fast doubling in Ruby:

def fibonacci(n)
  fib_hash = Hash.new do |h, k|
    h[k] = _fib(h, k)
  end
  fib_hash[0] = 0
  fib_hash[1] = 1
  fib_hash[2] = 1
  fib_hash[n]
end

def _fib(hash, n)
  half_n = n / 2
  a = hash[half_n + 1]
  b = hash[half_n]

  if n.odd?
    a * a + b * b
  else
    2 * a * b - b * b
  end
end

By leveraging the default proc for Hashes, we avoid redundant calculations. This is a useful tactic for dynamic programming.

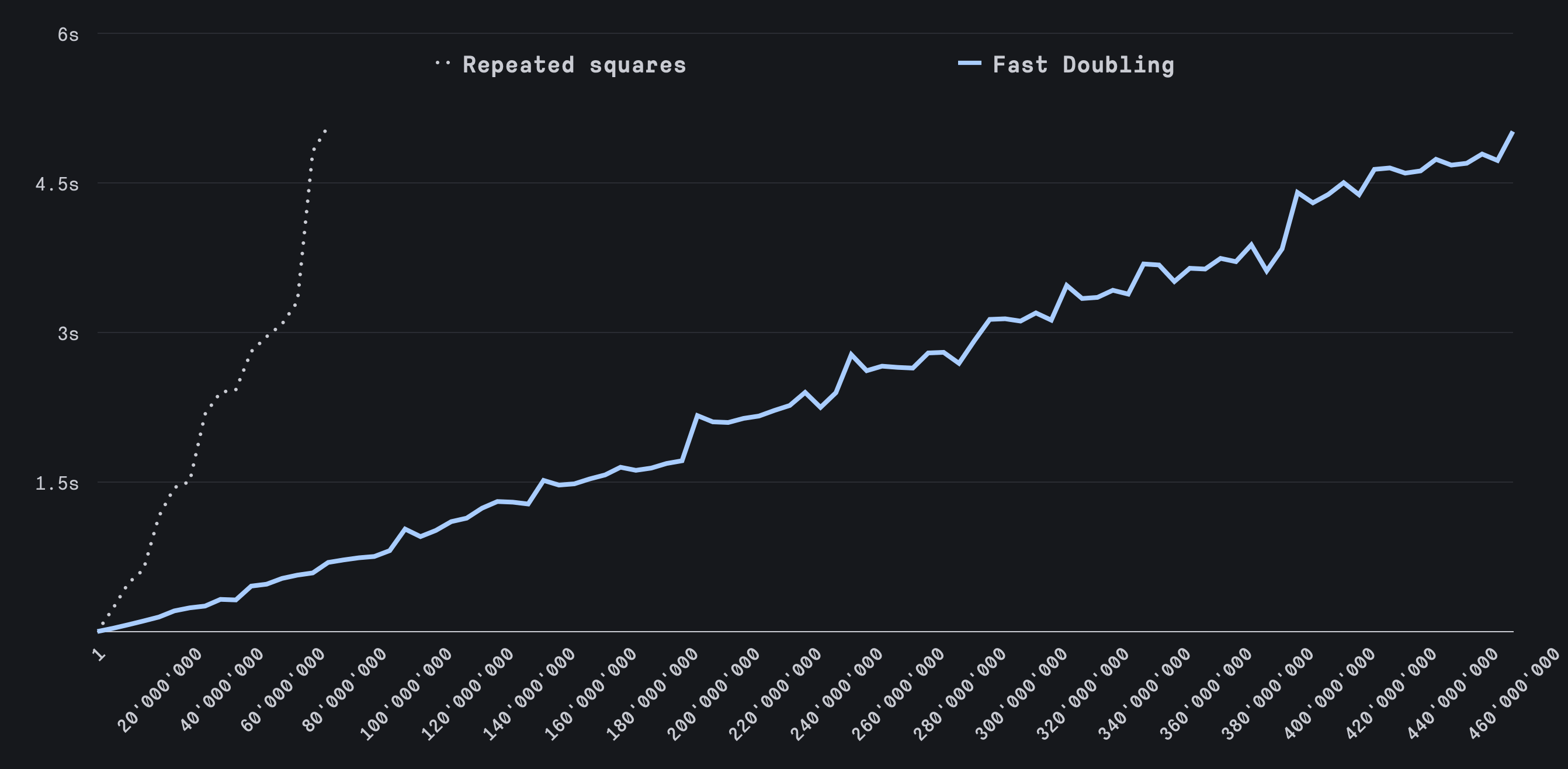
This is the most efficient algorithm we’ve explored. With it, we can compute the 1,000,000,000th Fibonacci number in just a few seconds.

Conclusion: Ruby and Fibonacci — A Perfect Match

From the naive recursive method to advanced matrix algebra and fast doubling, exploring Fibonacci numbers reveals a rich landscape of algorithms and optimizations. Ruby—with its expressive syntax and powerful libraries like BigDecimal, support for rationals, and tail call optimization—proves to be an excellent language for both learning and high-performance computation.

Whether you’re preparing for interviews, tackling mathematical challenges, or simply fascinated by algorithmic elegance, these Fibonacci funhouse techniques are valuable additions to your programming toolkit.

So next time someone asks you to write a Fibonacci algorithm, you can confidently say: “Yes—and here’s how to do it better.”